Abstract
A platform for providing access to games of chance over the internet that uses smart contracts to ensure the fairness and randomness of games in a manner that is visible to participants. Oversight by trusted third parties is therefore unnecessary to determine random outcomes and provide rewards to winning participants. Because true randomness does not exist in a computational setting, seed values may be used as inputs to a pseudo-random number generator (PRNG). These seeds, which are affected by the actions of different individuals at different times, may introduce entropy into the system, which may in turn be used to determine winning participants in a fair and random manner.
Introduction
Games of chance have entertained humankind for much of recorded history. In many cultures, games of chance have also facilitated the transfer of wealth through wagers on the outcomes of these games. The reason such games are a source of excitement, and are suitable for wagers related to their outcomes, is the randomness of the games. Humankind’s inability to know what will happen next creates excitement surrounding an outcome, and is what causes attempts to predict the outcome and place a wager to be a gamble.
In modern times, most organized acts of gambling are facilitated by trusted third parties, such as casinos or other sanctioned entities. These third parties, when honest, ensure that games are truly random, receive bets, retain the bets from individuals who place unsuccessful wagers, distribute winnings to individuals that place successful wagers, and usually retain a fee for performing one or more of these tasks.
In the seminal Bitcoin whitepaper, Satoshi Nakamoto notes the problems associated with reliance of internet commerce on trusted third parties – financial institutions in the case of Bitcoin – and proposes a system for internet commerce that uses cryptographic proof instead of trust, to enable transactions to occur without the need for the inefficiencies or costs associated with third parties.
In a similar vein, we propose to create a platform for engaging in games of chance over the internet using cryptocurrency-based smart contracts, eliminating the need for third party oversight. The public nature of smart contracts would enable all parties who take part to verify the randomness and fairness of the games, while eliminating the potential for human error or dishonesty that may exist when a third party is used. Use of computational resources rather than human entities would enable a potentially unlimited number of games to occur, near-continuous availability of such games, and implementation of games having characteristics that would be difficult or impossible for human entities to implement. Additionally, such games may be implemented in a more efficient and less expensive manner when compared to the use of trusted third parties.
Games
Gelotto is built on the Juno blockchain as a CosmWasm (CM) smart contract and as such will utilize cryptocurrency assets available to the Inter-Blockchain Communication Protocol (IBC) associated with the Cosmos ecosystem.
Initially, Gelotto will launch by offering a series of lottery games. Numerous types of games of chance exist, using random elements such as cards, dice, or more complicated electronic outputs such as those found in slot machines. Lottery games were selected because games that incorporate selection of a unique random number (or a random alphanumeric string or other type of unique data), common to such games as Bingo, Keno, and various raffles and lotteries, are suitable for simultaneous participation by a large number of participants. Additionally, lottery-type games are relatively simple to understand, having few rules to learn and limited actions required by a participant. Further, a lottery-type game may reach an outcome by performing only a single random determination: the selection of a random number (or multiple random numbers) that represents one or more winning participants.
In the future, other games such as slots or blackjack may be implemented. The methods described below with regard to participating in lottery games, starting and ending games, selection of random outcomes, and distribution of rewards, may also be applicable to future games.
Purchasing “Lottery Tickets”
Individuals will participate in a lottery by accessing the Gelotto platform to “purchase tickets” using a selected cryptocurrency asset. Because Gelotto is built on the Juno blockchain, the selected cryptocurrency asset would be among those that are enabled to access the IBC.
The cryptocurrency asset used to purchase tickets would be transferred from the participant’s wallet to a smart contract associated with the lottery game selected by the participant. The smart contract associated with the lottery game would receive assets from all participants and would ultimately serve as the prize pool that is used to distribute a reward to the winning participant(s).
To represent the transfer of assets from a participant to the smart contract associated with the lottery game, a data structure stored in the smart contract would be updated to associate the address of the participant’s wallet with a unique number that represents this transfer of assets in exchange for one or more tickets. Therefore, an actual “ticket” asset would not need to be generated to transfer to the participant. The data structure would serve as a record of tickets that were purchased by each participant.
Simplified Example
For each ticket that is purchased, the application for a lottery game may increment a counter. A first participant having the wallet address “ABC” may transfer sufficient assets to purchase one ticket. The application would increment the counter to “1” and associate the number 1 with the wallet address ABC. A second participant having the wallet address “DEF” may then transfer sufficient assets to purchase three tickets. The application would increment the counter to “2”, associate this number with the address DEF, increment the counter to “3” and associate that number with the address DEF, increment the counter to “4”, and so forth. The first participant may access the Gelotto platform a second time and transfer sufficient assets to purchase an additional ticket. The application would increment the counter to “5” and associate this number with the address ABC. A third participant with a wallet address of “GHI” may similarly purchase a ticket represented by the number “6”, which would be associated with the third participant’s wallet address. This process may continue until a lottery game is completed.
Continuing the example described above, assume that 202 tickets are purchased by various participants. See the table below for an example representation of tickets associated with such a lottery game:
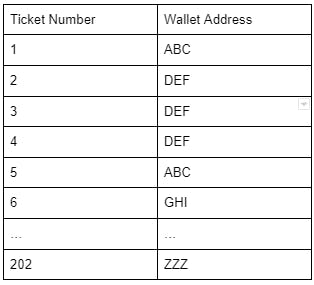
The example data structure above (shown as a table, though any type of data structure may be used), functions as a record of the cryptocurrency assets that were transferred from each participant to the smart contract associated with the selected lottery game. As such, each entry in this record may constitute a virtual “ticket” for the lottery game. Random selection of a ticket number would then be used to determine a winning participant, with each participant’s odds of winning being proportional to the number of tickets that were purchased by that participant, and inversely proportional to the total number of tickets purchased by all participants for the selected game. Of note, because the assets received for ticket purchases from all participants are used as a prize pool from which rewards are distributed, while the odds (per ticket) of winning would be smaller for a game having a larger number of participants, the size of the prize pool associated with the game would be larger than that of a game having fewer participants.
While the simplified example above illustrates a system in which a cumulative ticket counter is incremented by 1 each time a ticket is purchased, the platform may accommodate purchasing multiple tickets at one time by storing one entry within the data structure for each purchase transaction. In such a case, tickets that are purchased may represent intervals within the total set of ordered tickets. For example, a first participant with the wallet address “ABC” may purchase a single ticket, a second participant with the wallet address “DEF” may purchase ten tickets, and the first participant may then return to purchase four additional tickets. This may result in a data structure shown below.
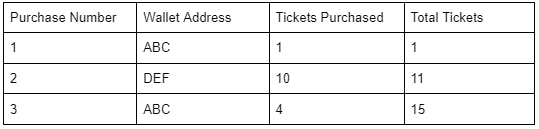
In such a case, each purchase of one or more tickets, represented in the table above by a purchase number, may be represented by an interval within the total set of tickets. In the example, the interval for Purchase Number 1 would be [0, 1), the interval for Purchase Number 2 would be [1, 10), and the interval for Purchase Number 3 would be [10, 15). A winning participant may be determined if a random number is selected that is within an interval associated with the participant. The data structure that records each ticket purchase may store each distinct ticket or group of tickets in the order that the ticket(s) are purchased, the wallet address of the participant, the number of tickets purchased, and the cumulative number of tickets that have been ordered.
Example code
struct TicketOrder {
owner: Addr, // player's address
count: u16, // number of tickets ordered
cum_count: u64, // cumulative count
}
Starting and Ending Lottery Games
Assets may be transferred from addresses associated with participants to the smart contract associated with a lottery game (“purchasing tickets”), and the data structure described above may be updated, during defined ranges of time when an option to purchase tickets for the selected game is active. For example, a recurring lottery game may take place over a selected time period, such as hourly, daily, weekly, or other selected time periods.
For a typical lottery game, the option to purchase tickets may become available at a selected time, and the option to purchase tickets may remain available until the game ends and a random ticket is selected by the smart contract. For example, for a game that is scheduled to occur hourly, participants may initially be provided with the option to purchase tickets once the previous hourly game has concluded. Participants may continue to purchase tickets for a time period of approximately one hour, after which the option to purchase tickets will end, one or more random numbers will be selected by the smart contract, and a reward will be transferred to the winning participant(s). This process may then repeat for the subsequent hourly lottery game.
In some cases, other timeframes may be used. For example, certain games may enable the purchase of tickets during specified time periods, independent of when previous games begin or end. Similarly, certain games may end the option to purchase tickets at a selected time, independent of the time when the winning participant(s) will be determined and independent of the start and end times of other games.
Integration of Randomness into the Games
A lottery game ends by selection of winning “tickets” in a manner that is unpredictable yet deterministic. In a computing environment, true randomness is often not possible to achieve. For example, neither block hash nor other block metadata are reliable sources of entropy. Many cryptocurrency projects that incorporate randomness must rely on use of cryptocurrency-based oracles, or trusted third parties. As noted above, Gelotto seeks to create a platform for engaging in games of chance using smart contracts, without reliance on external sources. Therefore, the Gelotto platform will incorporate a different method for creating entropy to enable random (or pseudo-random) determination of winners for each game.
To accomplish this goal, Gelotto will incorporate a concept of entropy-over-time. Specifically, when a participant purchases a ticket for a lottery game, the smart contract associated with this transfer of assets may update a seed value that is stored in state by combining its previous value with additional entropy. This seed may also be updated when a game ends. When a game ends and one or more random numbers must be selected to determine the winning participant(s), this seed may be an input to a pseudo-random number generator (PRNG), such as a Permuted Congruential Generator (PCG), which produces a deterministic sequence of uniformly distributed random numbers that ultimately map to one or more winning participants.
Specifically, when a contract is instantiated, it may initialize a seed using a hash of various game state elements, combined with block metadata. On each instance that a participant purchases one or more tickets, the existing seed may be combined and rehashed with new data, such as game state elements and block metadata at the time the purchase occurs, to form a new seed that replaces the existing one. This process may be repeated each time that a purchase of one or more tickets occurs, forming a chain of hashes, until the option to purchase new tickets is closed. Because the order and times at which tickets are purchased are determined by multiple participants who are mutually and equally involved in controlling the underlying game state, use of these purchases to update the seed value introduces entropy that the smart contract may harness in the winner selection process.
After the option to purchase new tickets is closed, the seed for the lottery game may be updated once more, using the process described above, then sent to a PRNG to select one or more numbers to determine the winning participant(s).
Example Code
use base64ct::{Base64, Encoding};
use cosmwasm_std::Addr;
use sha2::{Digest, Sha256};
/// Initialize the seeed when the contract is instantiated.
pub fn init(
game_id: &String,
block_height: u64,
) -> String {
let mut sha256 = Sha256::new();
sha256.update(game_id.as_bytes());
sha256.update(block_height.to_le_bytes());
let hash = sha256.finalize();
Base64::encode_string(&hash)
}
/// Update the seed when a participant
/// purchases one or more tickets.
pub fn update(
game: &Game,
player: &Addr,
ticket_count: u32,
lucky_string: &String,
block_height: u64,
) -> String {
let mut sha256 = Sha256::new();
sha256.update(game.seed.as_bytes()); // previous seed
sha256.update(player.as_bytes());
sha256.update(ticket_count.to_le_bytes());
sha256.update(lucky_string.as_bytes());
sha256.update(block_height.to_le_bytes());
let hash = sha256.finalize();
Base64::encode_string(&hash)
}
/// Update seed when the option to
/// purchase tickets ends.
pub fn finalize(
game: &Game,
sender: &Addr,
lucky_string: &String,
block_height: u64,
) -> String {
let mut sha256 = Sha256::new();
sha256.update(game.seed.as_bytes()); // previous seed
sha256.update(sender.as_bytes());
sha256.update(lucky_string.as_bytes());
sha256.update(block_height.to_le_bytes());
let hash = sha256.finalize();
Base64::encode_string(&hash)
}
Random Selection of Winning Participant(s)
Random numbers may be selected by using the seed as an input to a random number generator. The generated number(s) may be mapped to one or more specific participants based on the data structures that associate ticket numbers, or intervals associated with groups of purchased tickets, with those participants.
For example, in a lottery game where 202 tickets have been purchased, the random number generator may generate an integer ranging from 1 up to 202, depending on the final seed value that was determined using the methods described above. Once the random integer is generated, the particular wallet address associated with the random integer, or with the interval of numbers that includes the random integer, may be determined using the data structure for the lottery game.
The platform may use a “roulette wheel selection” method, also known as a fitness proportionate selection method, to select a random number. In this method, the probability of a participant being selected as a winner, denoted by the probability variable pi, is proportional to the number of tickets purchased by that participant, represented by the fitness variable fi. The probability is inversely proportional to the total number of tickets that were purchased by all participants, represented by the variable N.
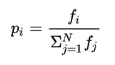
When a random number is selected, this number will correspond to a slot within a virtual roulette wheel. Each slot within the virtual wheel may be represented by an interval of purchased tickets, described above. The size of the slot is proportional to the number of tickets purchased in a transaction, and the slot that includes a winning ticket may be mapped to the wallet address of the participant that purchased the ticket.
Therefore, to select one or more winning participants, a contract may generate a random number between zero and the total number of tickets that were purchased. Once that number is determined, the contract may perform a binary search using the data structure to determine the wallet address associated with that number. This process is repeated to determine each winning participant.
Example Code
fn select_winner(
orders: &Vec<TicketOrder>, // full vec of ticket orders
n: usize, // number of winners to find
rng: &mut Pcg64 // random number generator
) -> usize {
let n_tickets_sold = orders[orders.len() - 1].cum_count;
let x = rng.next_u64() % n_tickets_sold;
bisect(&orders[..], orders.len(), x)
}
/// Perform binary search using bisection
/// to determine which interval contains `x`.
fn bisect(
orders: &[TicketOrder], // slice to search
n: usize, // length of slice
x: u64 // random value
) -> usize {
let i = n / 2;
let order = &orders[i];
let lower = order.cum_count - order.count as u64;
let upper = order.cum_count;
if x < lower {
// go left
return bisect(&orders[..i], i, x);
} else if x >= upper {
// go right
return bisect(&orders[i..], n - i, x);
}
i // return the index of the TicketOrder
}
Rewards to Winning Participant(s)
As described previously, the assets transferred from each participant to the smart contract associated with the lottery game are used as a prize pool from which a reward for the winning participant(s) is distributed.
In a typical game, 90% to 95% of the assets in the prize pool would be awarded to the winning participant(s). 5% to 10% of the assets would be retained for use in subsequent games that occur on the Gelotto platform, described below.
Games may include a single winner that receives the entire reward, or multiple winners that receive equal or unequal rewards. The number of winning participants and the portion of the prize pool that is distributed in each reward may be specific to each lottery game.
Rewards, when claimed by a winning participant, would be transferred to the wallet address that is associated with the ticket purchase that corresponds to the selected random number.
Mega Jackpot Games
Over the course of an extended period of time, such as weekly, monthly, annually or another selected time period, a portion of each prize pool for each of the recurring lottery games, such as 5% to 10%, may be retained for use in “mega jackpot” and “grand prize” games.
A mega jackpot game may constitute a lottery game that is similar to the games described above, in which random selection of a number corresponding to a ticket may be mapped to a wallet address for one or more winning participants, to which a reward may be distributed.
However, rather than using assets for a prize pool created by participants that purchase tickets, a mega jackpot game may distribute rewards from the portions of each prize pool that were retained from previous lottery games. For example, a portion of each lottery prize pool (such as 5 to 10 percent) may be retained as a “mega jackpot” prize pool. Once per week, one or more random numbers for a mega jackpot game may be selected, and a reward from this mega jackpot prize pool may be distributed to one or more winning participants. This reward is expected to be larger in value than rewards that may be won participating in other lottery games that occur more frequently.
Because the prize pool for a mega jackpot game does not require the purchase of tickets by participants, tickets for a mega jackpot game may be provided to participants using other criteria. For example, criteria for participation in a mega jackpot game may include previous participation in specific types of lottery games during a selected timeframe. Data structures for previous lottery games may serve as a record of such participation. For example, a ticket for participation in a mega jackpot game may be awarded to wallet addresses that have participated in a selected number of lottery games, lottery games associated with selected types of assets, lottery games associated with selected recurring timeframes, and so forth.
The criteria for participation in a mega jackpot game may be modified for each game, to add a sense of gamification to the Gelotto platform, and to incentivize participation in different available lottery games.
As such, recurring mega jackpot games may further incentivize participation in various other games on the Gelotto platform, and rewards for the mega jackpot games may be funded using assets received from participation in other games.
The Gelotto Token (GLTO) – Initial Distribution
The Gelotto platform will include a native token, Gelotto (GLTO), that will be used for a variety of purposes associated with the Gelotto platform. The GLTO token will be created as CW token on the Juno Blockchain.
Initially, the GLTO token will be distributed through an airdrop to wallets that own selected quantities of certain IBC assets.
GLTO will have a total supply of 420,690,000 tokens.
- 60% of this supply (252,414,000 tokens) will be distributed via airdrop.
- 15% of this supply (63,103,500) will be provided as incentives for liquidity pools that include the GLTO token.
- 15% of this supply (63,103,500) will be used as additional incentives for various games on the Gelotto platform. Any GLTO distributed by airdrop that is not claimed will be added to this portion of the supply.
- 10% of this supply (42,069,000) will be reserved for the Gelotto Development Team. This portion of the supply will be released over a period of 36 months, in equal amounts, once per month.
The Gelotto Token (GLTO) – Uses
The GLTO token will be usable on the Gelotto platform in the same manner as other cryptocurrency assets. For example, lottery games may be played in which tickets are purchased using GLTO, and a reward is paid to winning participant(s) using GLTO from the resulting prize pool. Portions of GLTO prize pools that are not distributed as rewards to winning participants may be used for mega jackpot games and other subsequent games.
GLTO may similarly be usable in future games, such as slots and blackjack, when such games are added to the platform.
The GLTO token may also be used as incentives for participation in various games. For example, GLTO may be added to a prize pool for one or more lottery games to incentivize participants to purchase tickets for those lottery games. As another example, GLTO tokens may be awarded to participants of certain games, independent of the outcome of the game.
At times, selected sums of the GLTO token may be exchanged to purchase tickets for other games, such as lottery games for other assets. GLTO tokens may also be usable to purchase NFTs associated with the Gelotto platform.
The GLTO token may be held to participate in governance of the Gelotto platform. For example, governance may be used to decide the parameters of lottery games that are available (such as the specific assets, the price per ticket, the timeframe during which a game recurs, and so forth). Governance may also be used to decide availability and parameters of future games.
The GLTO token is intended to have a special purpose for participation in annual “grand prize” games, described below.
Grand Prize Games
To incentivize participants to acquire and hold significant quantities of the GLTO token, annual “grand prize” games are intended to be conducted that include aspects that reward participants who have acquired and held quantities of the GLTO token. The grand prize games are intended to offer significant prizes (e.g., estimated values of 50,000 USD or more per prize). Funds for these prizes may be obtained using the portion of each lottery game prize pool that is not distributed as a reward to a winning participant (e.g., from 5% to 10% of each prize pool).
A description of one example grand prize game follows:
Every month, over the course of 12 months, snapshots will be taken to determine the amount of the GLTO token held by various wallets. Each wallet that holds at least a selected amount of the GLTO token will receive a selected quantity of a secondary cryptocurrency token: “keys” that may be used to open “locked chests” that contain prizes.
It is intended that 1000 keys will be distributed, with approximately 83.3 keys being distributed each month.
After distribution of the keys, access to the grand prize game will be enabled on the Gelotto platform. The grand prize game will present a number of virtual “locked chests” (from 10-20 locked chests). Each chest represents an unknown prize that is intended to have a value of at least 50,000 USD.
Using the Gelotto platform, participants may “unlock” a virtual locked chest by burning a number of keys. The first chest may be opened by burning a relatively small number of keys (such as 5 keys), while each subsequent chest may require a progressively larger number of keys to be opened. This process may encourage participants to exchange key assets with one another, create tools of trust, or collaborate in other ways.
Locked chests may include cryptocurrency assets, physical assets that may be physically provided to winning participants, fiat currencies, or other prizes.
The above describes one possible example of a grand prize game. Other types of games that offer significant prizes to incentivize accumulation of the GLTO token may also be implemented.
The Gelotto Token (GLTO) – Value Proposition
The act of investment in various assets, especially speculative investment assets such as cryptocurrency, represents a significant gamble. Individuals that invest in cryptocurrency tend to possess a large tolerance for risk and a large interest in games of chance. Such individuals may have a greater probability of choosing to participate in games offered by the Gelotto platform, and the acquisition of the GLTO token.
Many of the assets associated with the IBC offer periodic yields as incentives to accumulate and hold the assets. As such, an individual that receives a significant quantity of assets each day as part of a yield-based investment strategy is more likely to be willing to place a portion of such assets at risk through a game of chance than individuals who do not receive periodic incentive payments as part of an investment position. Individuals that receive frequent incentives due to investment in IBC-based cryptocurrency assets may be more likely to use a portion of these incentives to participate in ganges of chance.
Regular participation in games of chance may be seen as a stochastic (a system governed by probabilities) investment strategy. For example, the rewards received by a participant that wins one or more games, when considered over a period of time, may be similar to a rate of return on an investment that is akin to an interest rate.
The opportunity to accumulate the GLTO token as an investment asset, as a governance asset associated with the Gelotto platform, as an asset to purchase tickets, NFTs, and other valuable opportunities or assets using the Gelotto platform, and an asset to participate in grand prize games where significant prizes may be acquired, provides the GLTO token with at least a nominal value, that may increase significantly as larger numbers of participants utilize the Gelotto platform.
Conclusion
We have proposed a system for conducting games of chance over the internet that does not rely on trusted third parties. By using smart contracts to conduct such games, individuals that participate in the games may verify the randomness and fairness of the games, and the games that occur are not limited in quantity or scope in the same manner that games implemented by human entities would be limited.
Participants may therefore participate freely in a variety of lottery games, (and in the future, other games of chance), without requiring the oversight of trusted third parties. Incentives to participate in various games using the Gelotto platform, and to acquire and hold the GLTO token, may increase use of the Gelotto platform in a manner that rewards participants with a chance of a reward, in a manner that is visible owing to the smart contracts used to govern the platform.
